Beweisen schon in der Grundschule ? !

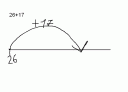
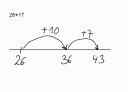
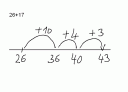
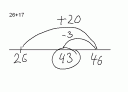
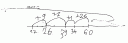
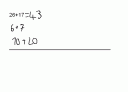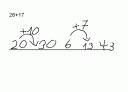Können Grundschulkinder schon einfache Beweise herleiten und verstehen wie z.B.:

Jede Summe aus drei aufeinanderfolgenden natürlichen Zahlen ist durch drei teilbar !

Beweisen kann man das indem man die Zahlen abstrakt beschreibt und dann umformt:

n + (n + 1) + (n + 2) = 3n + 3 die Zahl 3n + 3 ist natürlich durch 3 teilbar, was man sofort sieht.

Grundschulkinder sehen das natürlich nicht, man kann die algebraische Darstellung aber in eine anschauliche Form bringen:

n ist: … o
n+1: … o o
n+2: … o o o

Durch Umlegen des letzten Plättchens in die erste Reihe:

… o o
… o o
… o o

sieht man sofort, dass die Zahl durch 3 teilbar sein muss.

Man könnte jetzt auch untersuchen, wie das mit 4, 5, 6 , … aufeinanderfolgenden Zahlen aussieht.

4 aufeinanderfolgende Zahlen sind nämlich nicht durch 4 teilbar wie man sich sofort vorstellen kann,
wenn man das Zahlenbild-Muster in der Vorstellung umgruppiert, sondern allenfalls durch 2:

… o
… o o
… o o o
… o o o o

Bei diesem Verändern des Musters in Gedanken kommen dieselben Mechanismen zum Tragen,die wir auch nutzen, wenn wir mit Zahlen rechnen, also z.B. die Additionsaufgabe:

5 + 8

und dabei die Zahl 8 in 5 und 3 zerlegen um den Zehner voll zu machen:

5 + 5 + 3 = 10 + 3 = 13

hier spielen Muster und Strukturen eine Rolle, die sich auf konkrete strukturierte Mengenbilder beziehen:

o o o o o ‚plus‘ o o o o o o o o

denken wir als

o o o o o
o o o o o o o o also

10 + 3

Diese Denkmuster sind aber durch vielfältigen Gebrauch und durch Abstraktion, also durch die Loslösung von konkretem Material oder von konkreten Mengen, so unscharf und damit universell geworden, dass wir sie direkt auf Zahlen beziehen oder einfach nur wissen, dass das eben so ist.

Mathematik in der Grundschule ist Rechnen und Umgang mit Strukturen

Mathematik ist mehr als Rechnen‘, diesen Satz hört und liest man immer wieder. Wenn man allerdings den Mathematikunterricht betrachtet, dann geht es über weite Strecken aber doch nur um das ‚Rechnen können‘, also die Entwicklung von Rechenfertigkeit.Dieser Fokus auf die Rechenfertigkeit führt dann in der Folge häufig dazu, dass bei Rechnungen und auch im gesamten Mathematikunterricht auf das Ergebnis fokussiert wird und nicht auf den Rechenweg. Ob der Schüler effektiv, geschickt, schön und richtig gerechnet hat spielt keine Rolle sondern nur ob das Ergebnis richtig oder falsch ist.
Damit verliert man die Struktur der Rechnung, des Algorihmus, der Problemlösung aus dem Blick, obwohl gerade sie aufzeigt, wo der Schüler wirklich steht, wo er Probleme oder Stärken hat, wie flexibel er mathematische Problem lösen kann bzw. wie flexibel er beim Denken ist. Trotzdem muss man feststellen, dass nicht Algorithmen, also Rechenverfahren die zentrale Idee der Mathematik sind sondern Muster und Strukturen, die man Erkennen, Verändern (hier helfen eventuell Algorithmen), Aufbauen, … muss.
Das Erkennen von und flexible Umgehen mit Strukturen ist aber auch die Grundlage gut entwickelter Rechenfertigkeiten. Die Aufgabe 29 + 37 muss strukturiert werden:
2 Zehner 9 Einer (also fast ein Zehner) + 3 Zehner 7 Einer . Mit dieser Vorstellung kann man nun verschiedene Lösungswege beschreiten:
        2 Zehner + 3 Zehner + 9 Einer + 7 Einer = ….
        2 Zehner 9 Einer + 3 Zehner + 7 Einer = …
        2 Zehner 9 Einer + 7 Einer + 3 Zehner = …
        3 Zehner 7 Einer + 2 Zehner + 9 Einer = …
        3 Zehner 7 Einer + 3 Zehner – 1 Einer = …
Der umständlichste und aufwändigste Rechenweg ist dabei der erste (20+30+9+7), der geschickteste ist der letzte Rechenweg (37+30-1). Diesen Weg werden Kinder, die nur auf das Ergebnis fixiert rechnen und nicht auch versuchen zu einer Aufgabe viele Rechenwege zu finden allerdings nie entdecken, zumal auch viele Erwachsene, die Kindern bei Schwierigkeiten helfen eher den ersten Weg (Rechnen mit Stellen) wählen, da er sehr nah am schriftlichen Rechenverfahren der Addition ist.
Damit setzen sie die Kinder aber in eine Falle, die dann zuschnappt, wenn die Subtraktion behandelt wird. Wenn man die Struktur der Additionsstrategie auf eine Subtraktionsaufgabe anwendet, dann kann sie bei 65-24 noch funktionieren. Sobald aber Aufgaben vom Typ 65 – 27 kommen wird es kritisch. Hier rechnen viele Kinder zunaechst den Unterschied bei den Zehnern 6 – 2 = 4 Zehner und dnanach den Unterschied bei den Einern 7 – 5 = 2 Einer. Das Ergebnis wird 42 sein oder falls das Kind bemerkt hat, dass hier ein Zehner nach unten überschritten wird 32.
Weitere Beispiele zu Rechenstrategien von Kindern bei der Addition findet man in den folgenden Beispielbildern:
Rechnen mit Stellen (Z + Z + E + E)


Schrittweise Rechnen:



Ein Rechentrick:

Viele richtige Rechnungen, aber die Struktur nicht erkannt:

Schöne Strukturen und Zusammenhänge kann man allerdings erst entdecken, wenn man nicht einzelne Aufgaben strukturiert, sondern Aufgabenpäckchen wie z. B.:
23 + 45 =                 76 – 35 =                 76 – 35 =
22 + 46 =                 75 – 36 =                 75 – 34 =
21 + 47 =                 74 – 37 =                 74 – 33 =
…………                 …………                …………

Wie sind die Päckchen strukturiert? Wie geht es weiter? Wie könnten ähnliche Päckchen aussehen? Welche Zusammenhänge kann man erkennen und warum ist das so?
Viele Fragen, die alle darauf zielen, die Schüler zu befähigen, Zusammenhänge / Strukturen zu entdecken, zu erforschen und Mathematik als das zu betreiben, was es eigentlich ist: ein interessantes Spiel mit Zahlen, Mustern und Strukturen.

Zusammenhang Addition – Subtraktion (Mengenoperationen)

In der fachdidaktischen Literatur liest man, dass Addition und Subtraktion eng zusammenhängen – Subtraktion ist die Gegenoperation zur Addititon und umgekehrt. Diese Argumentation bezieht sich auf die syntaktisch mathematische Struktur der Operationen: 4 + 5 = 9 oder 5 + 4 = 9 also ist 9 – 5 = 4 und 9 – 4 = 5. Damit wird auch unterstellt, dass Kinder, die die Addition erlernt haben, automatisch auch die Subtraktion verstehen und beherrschen. Leider zeigt die tägliche Praxis, dass man davon nicht ausgehen kann.
Die Addition wird immer noch hauptsächlich als Mengenoperation (Vereinigung disjunkter Mengen) eingeführt. Dabei vereinigen die Kinder z.B. eine Menge von 4 Steckwürfeln mit einer Menge, die aus 5 Steckwürfelchen besteht. Man erhält einen Würfelturm aus 9 Steckwürfeln. Da die Kinder viele solcher Materialhandlungen durchführen und dabei jeweils Zahlen (im Beispiel 5 und 4) Mengen zugeordnet werden, lernen Kinder , dass die Zahlen der Aufgabe 5 + 4 = __ durch 2 Mengen repräsentiert werden können, eine 5er Menge und eine 4er Menge, die zunächst getrennt hergestellt und betrachtet werden müssen, also nichts miteinander zu tun haben (disjunkt sind). Erst durch die Operation Addition, in der Aufgabe durch das + Zeichen notiert, werden die beiden Mengen quasi zu einer größeren Menge, dem Ergebnis verschmolzen. Wenn Kinder diese Vorstellungen entwickeln, also die Zahlherstellung (5er Menge herstellen) verbunden mit der Vorstellung der Operation Additon mit disjunkten Mengen, sind sie zunächst, bei allen Additionsaufgaben, erfolgreich.
Dieses Wissen und diese Vorstellungen nun auf die Subtraktion als Mengenoperation übertragen funktioniert nicht und führt zum Fehlkonzept disjunkte Mengen bei der Subtraktion. Für die Repräsentation der Aufgabe 9 – 5 stellen die Kinder wie von der Addition gewohnt die 9er Menge und die 5er Menge her und tappen in die Falle. Die Subtraktion ist nämlich keine Operation mit disjukten Mengen sondern eine Teilmengenbildung – ich nehme von einer vorgegebenen Menge eine bestimmte Anzahl Elemente weg. In unserem Beispiel würden die Kinder also nur die 9er Menge legen und diese dann in eine 5er und die Restmenge strukturieren. Das Ergebnis wird hergestellt, indem man dann noch die 5er Menge wegnimmt. Eine 4er Menge bleibt übrig.
Auf den Unterricht bezogen bedeutet das, man muss die Operationen Addition und Subtraktion zunächst als völlig unterschiedliche Operationen sehen, zwischen denen, auf der Mengenebene betrachtet semantisch Welten liegen. Vermeiden kann man die obern beschriebenen Fehlvorstellungen, wenn man den Zahlherstellungsakt (Mengen legen) zunächst nur für einen Summanden durchführt und die Operation immer nur auf dieser einen Menge ausführen lässt:
Aufgabe 4 + 5 =__ : die Kinder legen zunächst die 4er Menge und interpretieren + 5 als: ‚Lege noch eine 5er Menge zu der vorhandenen 4er Menge‘.
Aufgabe 9 – 5 =__ : die Kinder legen zunächstz die 9er Menge und interpretieren – 5 als: ‚ Nehme eine 5er Menge von der vorhandenen 9er Menge weg‘.
Diese eher operative Sichtweise 4 (+5) = 9 bzw. 9 (-5) = 4 ist dann auch geeignet, den Zusammenhang zwischen Subtraktion und Addition sowohl auf syntaktischen und wie auch semantisch deutlich zu machen.

Zusammenfassen von Dingen – Subitizing und Abzählen

Ein Beispiel zur Einführung:
Ein Kind bekommt zum Geburtstag Fingerpuppen geschenkt: Lehrer, Kaspar, Oma sowie Hund und Krokodil. Es hat also 3 Personen und 2 Tiere, also insgesamt 5 Figuren, die es auf die 5 Finger einer Hand stecken kann … 3 + 2 = 5. Diese Rechnung kann nun konkret auf die Fingerpuppen bezogen werden, man könnte aber auch sagen hier hat jemand die Anzahl der gekauften Gebäckstücke beim Bäcker berechnet, nämlich 3 Brezeln und 2 Brötchen oder sonst irgendein Beispiel in dem die Anzahlen 2 und 3 eine Rolle spielen.
Die im Beispiel beschriebenen Zusammenfassungen (Fingerpuppen , Gebäckstücke, …) kann man bei diesen kleinen Anzahlen natürlich mit den realen, gezeichneten oder gedachten Objekten machen. Wenn man dann aber irgendwann einmal 300 Brezeln und 200 Brötchen hat, was ja für eine Bäckerei kleine Anzahlen sind, kann man nicht mehr direkt mit den Objekten operieren sondern nur noch auf der Zahlenebene, also abstrakt, losgelöst von konkreten Gegenständen.
Um Rechnen zu können braucht man Zahlen und Zahlen erhält man z.B durch Mengenbildungen und dann durch Abstraktion von konkreten Mengen mit realen Objekten. Das Zusammenfassen von Objekten, reale, ikonische oder gedachte, wird als Mengenbildung beschrieben. Es muss klar sein, welche Objekte zu der Auswahl gehören und die einzelnen Objekte müssen unterscheidbar sein, da man sonst die Menge nicht genau abzählen könnte. Die Zahlen sind zunächst noch an die Objekte der Menge gebunden ( 3 Brezeln, 2 Tiere, 5 Bonbons, …) und werden dann aber davon gelöst, also abstrahiert. Man gebraucht dann eben nur noch die reine Anzahleigenschaft losgelöst von den Objekten, die dann wieder durch beliebige Objekte veranschaulicht werden kann.
Die Bestimmung der Anzahl von Objekten einer Menge kann durch Abzählen oder auch durch direktes Abschätzen (Subitizing) durchgeführt werden (siehe z.B.: Dehaene 1999, Der Zahlensinn). Dehaene geht ja von einem angeborenen Zahlensinn aus, auch bei Tieren, der dazu führt dass Objektanzahlen bis 3 direkt erkannt werden. durch Training und Kontextwissen lässt sich diese Fähigkeit aber weiterentwickeln:
– Kinder die Würfelspiele machen erkennen sofort die Würfelfünf oder Würfelsechs, auch ohne die einzelnen Punkte abzuzählen. – Skatspieler erkennen den Wert von Spielkarten z.B. 9, 10, 8, … ohne die Einzelsymbolde zu zählen
Mengen mit mehr als 3 Objekten müssen also eine besondere Anordung haben oder man muss diese Mengen in Teilen denken. Man muss die Mengen also irgendwie strukturieren. Dieses Strukturieren kann bei realen Objekten durch ändern der Anordnung (z.B. Reihen legen) oder durch die Bildung von Teilmengen (z.B. 5er legen), die man dann mit einem Blick erfassen kann. Bei gezeichneten Objekten z.B. durch Umkreisen von Teilmengen. Diese Aktivitäten können aber auch nur mental durchgeführt werden, man denkt sich die Teilmengen oder die Strukturen und ändert sie dann nach Bedarf.
Wahrscheinlich wird man auch eine 5er Menge die nicht strukturiert ist wie das Wuerfelbild bei der Anzahlbestimmung schnell in eine Dreier- und Zweiergruppen strukturiert und so als 5 erkannt.
Fazit: Die Anzahlbestimmung von strukturierten und unstrukturierten Mengen ist sehr stark uebungsabhaengig. Uebungen dazu werden z.B. bei ‚Blitzrechnen‘ angeboten.

Lernen von Mathematik – 1×1

Es wurde die Frage gestellt, ob man die Gedächtnisleistung beim Lernen von Einmaleinssätzchen (1×1) über ein System von Körperbewegungen verbessern könne.
Ich kenne kein solches System und bezweifle auch, dass das gut funktionieren koennte, da bei den 1×1 Saetzen sprachliche, ordinale, kardinale und auch geometrische Muster und Vorstellungen eine Rolle spielen. Das Konzept Arithmetik als Bewegung (Körpermetapher z.B. bei Lakoff/Nunez 2000: Where Mathematics comes from) beschreibt grundlegende Arithmetik wie z.B. vorwaertsgehen – vorwaertszaehlen oder rueckweartsgehen – rueckwaertszaehlen, usw …
Da es sich bei den 1×1 Saetzen zunächst um eine ueberwiegend sprachliche Gedächtnisleistungen handelt (siehe Dehaene 1999: Der Zahlensinn ..) koennen hier aber alle didaktisch-methodischen Kniffe der Sprachdidaktik eingesetzt werden. Also z.B. Anknüpfen an Bilder, Reimformen, sprachrhythmische Hilfen, … usw.
Falls das Kind dann die 1×1 Saetze lernt hat es aber immer noch keine Zahlvorstellung sondern eigentlich kontextloses Wissen erworben, was dann z.B. beim Loesen von Sachaufgaben mit z.B. multiplikativem Kontext zu Problemen fuehrt. Meiner Meinung nach ist deshalb der bessere Weg, der aber auch aufwendiger ist, zunaechst Zahlvorstellungen aufzubauen (z.B. mit Zehnerfeldkarten oder Punktefeldern).
Wenn dann solche Zahlenbilder als integrierte ordinal-kardinale Konzepte im Kopf vorhanden sind, mit denen das Kind auch mental operieren kann, dann kann man damit langsam Einmaleinsvorstellungen über das Verdoppeln und dann das Vervielfachen sowie über Nachbaraufgaben aufbauen (siehe Konzept Königsaufgaben des 1×1). Dabei muessen dann Grundaufgaben des 1+1 ohne großen mentalen Aufwand referiert werden koennen, um dann daraus das mentale Konzept 1×1/Multiplikation aufbauen zu können. Das ist also ein integriertes Konzept mit vielen Facetten.
Ein weiterer Ansatz, falls das Kind wirklich unter Gedaechtnisschwierigkeiten leidet (das muesste man pruefen – auch ob das Kurzzeit- oder eher Langzeitgedaechtnis betroffen ist, da dies ganz unterschiedliche Auswirkungen hat) waere Gedaechtnisuebungen und Konzentrationsuebungen durchzufuehren, also an den Ursachen zu arbeiten und nicht an den aktuellen Symptomen.

Fazit: es ist schwierig, eine Ferndiagnose zu stellen!